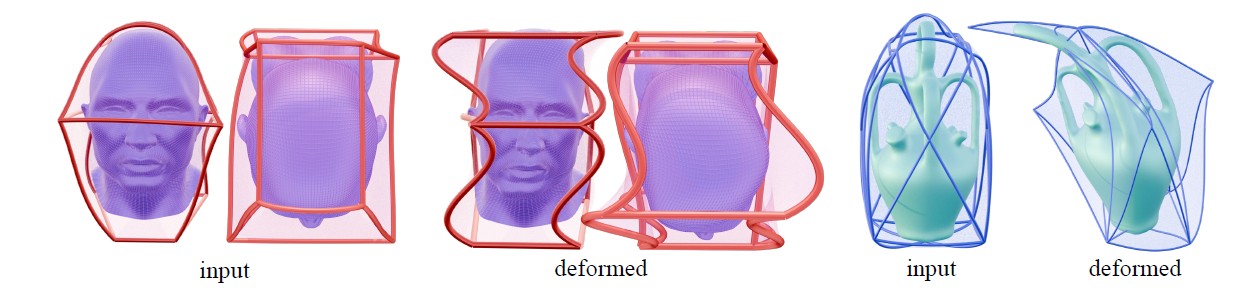
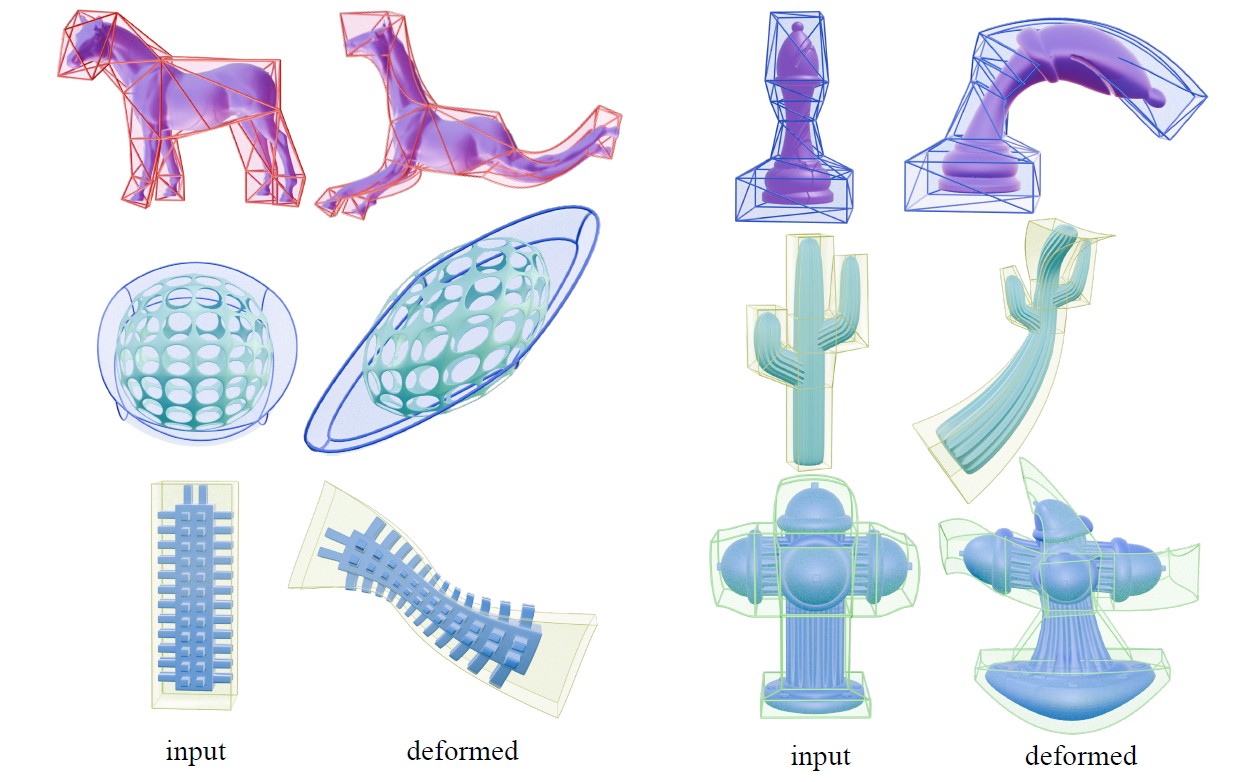
Cage-based deformation is a fundamental problem in geometry processing, where a cage, a user-specified boundary of a region, is used to deform the ambient space of a given mesh. Traditional 3D cages are typically composed of triangles and quads. While quads can represent non-planar regions when their four corners are not coplanar, they form ruled surfaces with straight isoparametric curves, which limits their ability to handle curved and high-curvature deformations. In this work, we extend the cage for curved boundaries using Bézier patches, enabling flexible and high-curvature deformations with only a few control points. The higher-order structure of the Bézier patch also allows for the creation of a more compact and precise curved cage for the input model. Based on Green’s third identity, we derive the Green coordinates for the Bézier cage, achieving shape-preserving deformation with smooth surface boundaries. These coordinates are defined based on the vertex positions and normals of the Bézier control net. Given that the coordinates are approximately calculated through the Riemann summation, we propose a global projection technique to ensure that the coordinates accurately conform to the linear reproduction property. Experimental results show that our method achieves high performance in handling curved and high-curvature deformations.